Calculating resistors for a 20-switch matrix
I used the technique described in Calculating a resistor network to work out a set of resistors for a 20-key matrix. Here's the program modified for this circuit:
(defparameter e6
'(100 150 220 330 470 680 1000 10 15 22 33 47 68))
(defun matrix (e6)
(let ((bestmin 0)
values)
(flet ((pushvalue (value)
(push (truncate (* 1024 value)) values)))
(dolist (a e6)
(dolist (b e6)
(format t "--- ~a ~a~%" a b)
(dolist (c e6)
(dolist (d e6)
(dolist (e e6)
(dolist (f e6)
(dolist (g e6)
(dolist (h e6)
(setq values nil)
(pushvalue (/ (+ b c d e f g h) (+ a b c d e f g h)))
(pushvalue (/ (+ b c d f g h) (+ a b c d f g h)))
(pushvalue (/ (+ b c f g h) (+ a b c f g h)))
(pushvalue (/ (+ b f g h) (+ a b f g h)))
(pushvalue (/ (+ f g h) (+ a f g h)))
;;
(pushvalue (/ (+ b c d e g h) (+ a b c d e g h)))
(pushvalue (/ (+ b c d g h) (+ a b c d g h)))
(pushvalue (/ (+ b c g h) (+ a b c g h)))
(pushvalue (/ (+ b g h) (+ a b g h)))
(pushvalue (/ (+ g h) (+ a g h)))
;;
(pushvalue (/ (+ b c d e h) (+ a b c d e h)))
(pushvalue (/ (+ b c d h) (+ a b c d h)))
(pushvalue (/ (+ b c h) (+ a b c h)))
(pushvalue (/ (+ b h) (+ a b h)))
(pushvalue (/ (+ h) (+ a h)))
;;
(pushvalue (/ (+ b c d e) (+ a b c d e)))
(pushvalue (/ (+ b c d) (+ a b c d)))
(pushvalue (/ (+ b c) (+ a b c)))
(pushvalue (/ (+ b) (+ a b)))
(pushvalue (/ (+) (+ a)))
;;
(let* ((sorted (sort values #'<))
(min most-positive-fixnum))
(mapl #'(lambda (x)
(when (second x)
(let ((diff (- (second x) (first x))))
(when (< diff min) (setq min diff)))))
sorted)
(when (> min bestmin) (setq bestmin min)
(format t "~a (~a ~a ~a ~a ~a ~a ~a ~a)~%"
min a b c d e f g h))))))))))))))
Because this program ran substantially slower than the version for 16 switches I made the code to check each set of candidate values a bit more efficient, but I'm sure it could be improved further.
The best output was:
24 (270 47 47 82 100 330 33 27)
Since you can multiply these values by an arbitrary factor I chose the values a = 27kΩ, b = 4.7kΩ, c = 4.7kΩ, d = 8.2kΩ, e = 10kΩ, f = 33kΩ, g = 3.3kΩ, and h = 2.7kΩ. Here's the final circuit:
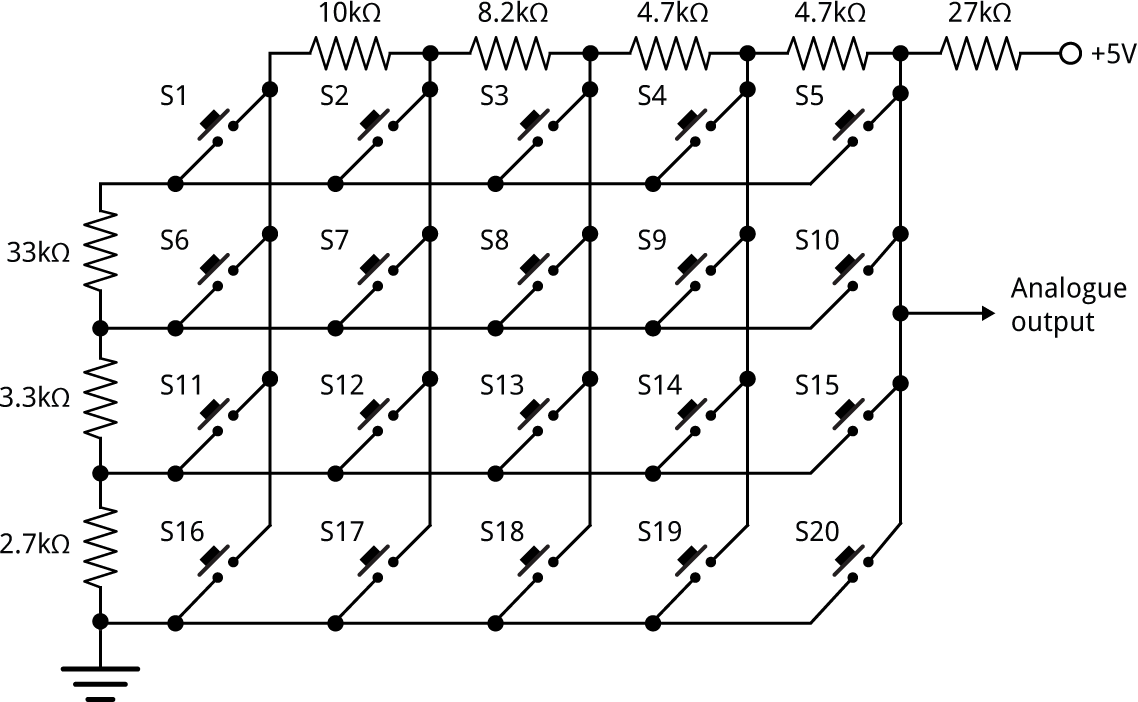
Postscript
If you're curious about why I wanted this, here's the application: Tiny Machine-Code Monitor.
blog comments powered by Disqus
