Lisp through the looking-glass
26th November 2017
The most fundamental construct in Lisp is the list, implemented as a linked list of cons cells, represented in every Lisp textbook with a diagram like this:
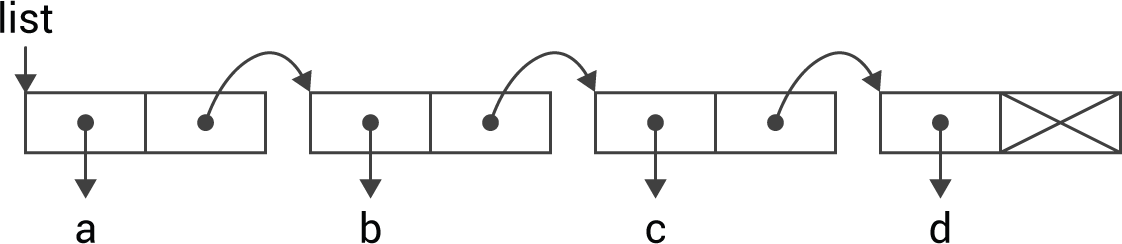
which, of course, is the internal representation for the list:
(a b c d)
Looking-Glass Lisp
However, Lisp could equally well have been implemented with the lists going right to left, rather than left to right. So in Looking-Glass Land the internal representation for this list would be:
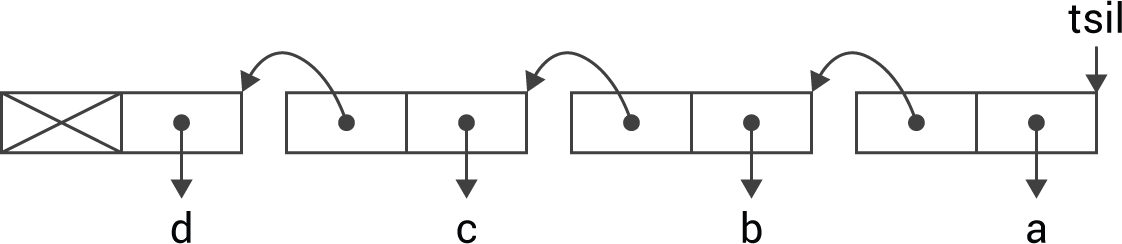
In normal Lisp this has the representation:
((((nil . d) . c) . b) . a)
Exploring this a bit further, let's write the Looking-Glass equivalents of first, rest, and cons. Initially I decided to call these tsrif, tser, and snoc, but that soon became a bit annoying, so I settled on ~first, ~rest, and ~cons.
Here are the definitions:
(defun ~first (list) (cdr list)) (defun ~rest (list) (car list)) (defun ~cons (a d) (cons d a))
Next, here's a function ~ to convert a list in normal Lisp representation to Looking-Glass representation:
(defun ~ (list) (cond ((null list) nil) (t (cons (~ (cdr list)) (car list)))))
For example:
CL-USER > (~ '(a b c d)) ((((nil . d) . c) . b) . a)
Defining a reader macro
For convenience, we can define { and } as reader macros to represent Looking-Glass lists:
(set-macro-character #\{ '~list-reader)
(set-macro-character #\} (get-macro-character #\) nil))
(defun ~list-reader (stream char)
(declare (ignore char))
(~ (read-delimited-list #\} stream t)))
This defines { as a macro character that calls ~list-reader, and } as a second macro character that behaves like ). So now we can write:
CL-USER > '{a b c d}
((((nil . d) . c) . b) . a)
Longest Common Subsequence
Finally, to prove that this alternative Looking-Glass representation works just as well as the standard representation, here's a Looking-Glass version of the recursive Longest Common Subsequence routine I presented in the earlier article Longest Common Subsequence. It finds the longest sequence of elements that occur in the same order in both sequences, and is called ~lcs.
First we need to define ~length:
(defun ~length (list) (cond ((null list) 0) (t (1+ (~length (~rest list))))))
Then here's the definition of ~lcs:
(defun ~longest (a b)
(if (> (~length a) (~length b)) a b))
(defun ~lcs (a b)
(cond
((or (null a) (null b)) nil)
((eql (~first a) (~first b))
(~cons (~first a) (~lcs (~rest a) (~rest b))))
(t (~longest (~lcs a (~rest b)) (~lcs (~rest a) b)))))
Trying it out:
CL-USER > (~lcs '{1 2 3 5 6 8 9} '{2 3 1 4 6 7 8})
((((nil . 8) . 6) . 3) . 2)
In other words,
{2 3 6 8}
which is the correct answer.
blog comments powered by Disqus
