Longest Common Subsequence
30th August 2016
I was recently writing a maze-solving program, and wanted a way to display the route through the maze when there were two or more paths of minimum length. For example, here's a simple Arrow Maze with two solutions:

Start on the arrow in the top left corner. From that arrow move to any one of the arrows it's pointing to, in the same row, column, or diagonal. Continue in this way, following successive arrows, and find the shortest route to the target in the bottom right corner.
Longest Common Subsequence
The solution to displaying the difference between two paths is first to find the Longest Common Subsequence (LCS) of the two paths; in other words, the longest sequence of elements that occur in the same order in both sequences.
The most efficient algorithm for finding the Longest Common Subsequence uses a matrix [1], but as usual there's a simpler, more intuitive solution using recursion which is ideal for my maze-solving problem. It's adequate for short lists, but wouldn't be efficient enough for applications such as finding the differences between two text documents.
Here's the routine:
(defun lcs (a b)
(cond
((or (null a) (null b)) nil)
((eql (car a) (car b))
(cons (car a) (lcs (cdr a) (cdr b))))
(t (longest (lcs a (rest b)) (lcs (rest a) b)))))
The algorithm works as follows:
- If the two lists have the same first element, the LCS is this followed by the LCS of the lists with the first element removed.
- Otherwise try ignoring the first element of each list in turn. The LCS is the one that gives the longest result.
It uses longest, which returns the longer of two lists:
(defun longest (a b) (if (> (length a) (length b)) a b))
Difference between two sequences
Once we have the LCS of two sequences, displaying the differences is relatively easy:
(defun diff (a b)
(let ((lcs (lcs a b))
result (pa 0) (pb 0))
(dolist (c lcs)
(let* ((qa (position c a :start pa))
(qb (position c b :start pb)))
(awhen (subseq a pa qa) (push (cons '- it) result))
(awhen (subseq b pb qb) (push (cons '+ it) result))
(push c result)
(setq pa (1+ qa) pb (1+ qb))))
(awhen (subseq a pa) (push (cons '- it) result))
(awhen (subseq b pb) (push (cons '+ it) result))
(nreverse result)))
This uses Paul Graham's "anaphoric macro" awhen from his book On Lisp [2]:
(defmacro awhen (test-form &body body)
`(let ((it ,test-form))
(when ,test-form ,@body)))
This is exactly like when, but lets you refer to the test form as it within the body of the awhen.
The function diff works by comparing the two lists with the LCS, and displays additions prefixed with "+" and removals prefixed with "-".
Solving the maze
The two solutions are:

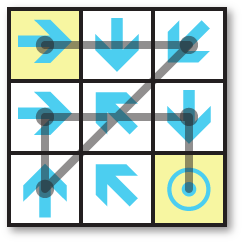
These could be represented as the lists (1 2 8 4 6 9) and (1 3 7 4 6 9), where the cells are numbered 1 to 9 starting in the top left corner. So to display the difference we can do:
(diff '(1 2 8 4 6 9) '(1 3 7 4 6 9))
This displays the result:
(1 (- 2 8) (+ 3 7) 4 6 9)
- ^ Longest Common Subsequence problem on Wikipedia.
- ^ Graham, Paul. On Lisp. Prentice Hall, 1993.
blog comments powered by Disqus
