Solving resistor networks
25th July 2018
I thought it shouldn’t be too difficult to write a Lisp program to calculate the resistance of a resistor network such as:
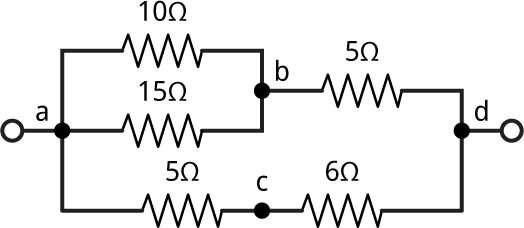
One way would be to define Lisp functions to calculate the resistance of two resistors in series, and of two resistors in parallel:
(defun series (x y) (+ x y)) (defun parallel (x y) (/ (+ (/ x) (/ y))))
Note that in Lisp (/ x) is a shorter way of writing (/ 1 x).
Now we can use these functions to express the complete circuit:
> (parallel (series 5 6) (series (parallel 10 15) 5)) 11/2
and the answer is 11/2 or 5.5 Ω.
A more general way of representing a network
This approach seems like it's getting the user to do most of the work. A more intuitive and general way to represent a resistor network would be to label each of the nodes a, b, c, etc and then represent it as a list of the resistances between each pair of nodes. Using this approach the above network becomes:
(defparameter *circuit* '((a d ?) (a b 10) (b a 15) (b d 5) (a c 5) (c d 6)))
The list (a d ?) represents the resistance we want to calculate.
All possible divisions of a set into two subsets
It will be useful to have a function split-set, that takes a list and an index i, and returns the ith division of the set into two subsets.
(defun split-set (list i)
(let (in out (ll (reverse list)))
(dotimes (j (length list))
(if (oddp i) (push (nth j ll) in) (push (nth j ll) out))
(setq i (ash i -1)))
(values in out)))
For a list of length n the total possible number of subsets is 2n. The function split-set works by expressing the index i as a binary number, and it then puts each element into one of the two sets according to whether the bit corresponding to that element is a 0 or a 1. So, for example, 13 in binary is 1101 so the 13th split of the list of four elements (a b c d) is:
CL-USER > (split-set '(a b c d) 13) (A B D) (C)
Combining parallel and series resistors
To simplify the network we successively combine pairs of resistors according to the rules of parallel and series resistors. To do this we look at every possible pair of resistors and see if they can be combined into a single resistor. For example, the two parallel resistors between a and b could be merged into a single resistor.
Here's the routine series-parallel to combine two resistors x and y. It also takes the entire circuit as a parameter so we can check for other connections between the same nodes:
(defun series-parallel (l x y)
(cond
((or (eq (caddr x) '?) (eq (caddr y) '?))
nil)
;; Check four possible labellings
((dolist (x (list x (list (second x) (first x) (third x))))
(dolist (y (list y (list (second y) (first y) (third y))))
;; Resistors in parallel
(when (and (eq (first x) (first y))
(eq (second x) (second y)))
(return-from series-parallel
(list
(list
(first x) (second x) (/ (+ (/ (third x)) (/ (third y))))))))
;; Resistors in series
(when (and (eq (first x) (first y))
(= (countlinks l (first x)) 2)
(not (eq (second x) (second y))))
(return-from series-parallel
(list (list (second x) (second y) (+ (third x) (third y)))))))))
(t nil)))
For two resistors in parallel we simply need to check that their start and end nodes are the same. For example, here it combines the resistors between a and b:
CL-USER > (series-parallel *circuit* '(a b 10) '(b a 15)) ((A B 6))
For two resistors in series we also need to check that no other resistor is connected to the node between the two resistors; this is what countlinks does:
(defun countlinks (l x) (count-if #'(lambda (i) (or (eq x (first i)) (eq x (second i)))) l))
For example, here we combine the two resistors between a, c, and d:
CL-USER > (series-parallel *circuit* '(a c 5) '(c d 6)) ((A D 11))
If it's not possible to combine the resistors series-parallel returns nil:
CL-USER > (series-parallel *circuit* '(a b 10) '(b d 5)) NIL
Simplifying a circuit
To simplify a circuit we use split-set to check every possible pair of resistors to see if they can be combined by series-parallel:
(defun simplify (list function n)
(let* ((l (length list))
(k (expt 2 l)))
(dotimes (i k list)
(multiple-value-bind (in out) (split-set list i)
(when (= (length in) n)
(let ((c (apply function list in)))
(when c (return (append c out)))))))))
This function simplify takes a list representing the network, a function for combining resistors, and a number of resistors to combine, and returns the simplified network.
Finally to solve the network we call simplify repeatedly until there's no more work to do:
(defun solve (circuit)
(let (len)
(loop
(setq len (length circuit))
(setq circuit (simplify circuit #'series-parallel 2))
(when (= (length circuit) len) (return)))
circuit))
Here it is working on the above network:
CL-USER > (solve *circuit*) ((A D 11/2) (A D ?))
So the network reduces to a single resistor of 5.5Ω.
A hitch
I thought I'd solved the problem, but then discovered that there are some networks that this approach can't solve. For example:
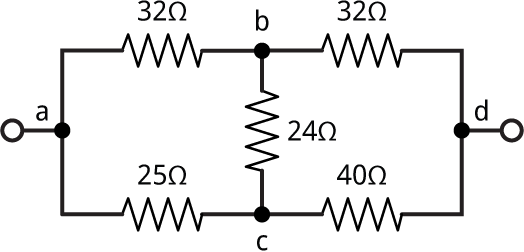
This can be represented as the list:
(defparameter *c2* '((a d ?) (a b 32) (b c 24) (a c 25) (b d 32) (c d 40)))
Trying to solve it gives:
CL-USER > (solve *c2*) ((A D ?) (A B 32) (B C 24) (A C 25) (B D 32) (C D 40))
It fails because the circuit doesn't contain any series or parallel configurations that can be simplified.
The solution is to do what's called a Delta-Wye transformation, which converts a triangle configuration, or delta, into a Y or wye configuration by adding an extra node [1]:
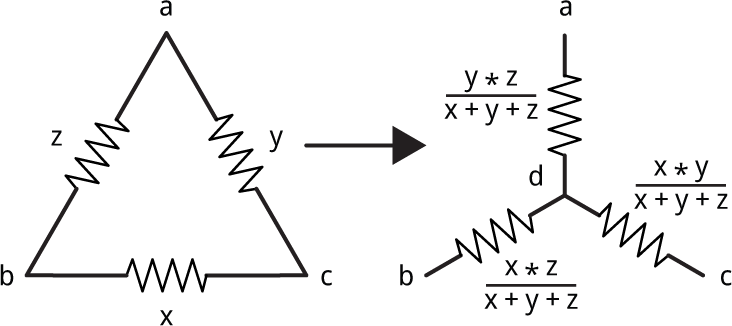
To solve these configurations the function delta-wye checks three links, and if they qualify as a delta network, they are transformed into a wye:
(defun delta-wye (l x y z)
(declare (ignore l))
(cond
((or (eq (caddr x) '?) (eq (caddr y) '?) (eq (caddr z) '?))
nil)
;; Check eight possible labellings
((dolist (x (list x (list (second x) (first x) (third x))))
(dolist (y (list y (list (second y) (first y) (third y))))
(dolist (z (list z (list (second z) (first z) (third z))))
(when (and (eq (first x) (second z))
(eq (first y) (second x))
(eq (first z) (second y)))
(let ((sum (+ (third x) (third y) (third z)))
(newsymbol (gensym)))
(return-from delta-wye
(list
(list
(first x) newsymbol (/ (* (third x) (third z)) sum))
(list
(first y) newsymbol (/ (* (third x) (third y)) sum))
(list
(first z) newsymbol (/ (* (third y) (third z)) sum))))))))))
(t nil)))
The function delta-wye uses a gensym for the fourth node.
Testing it with x=1, y=2, and z=3 gives:
CL-USER > (delta-wye nil '(a b 3) '(b c 1) '(c a 2)) ((A #:G847 1) (B #:G847 1/2) (C #:G847 1/3))
The solve function can be updated to incorporate delta-wye as follows:
(defun solve (circuit)
(let (len)
(loop
(setq len (length circuit))
(setq circuit (simplify circuit #'delta-wye 3))
(setq circuit (simplify circuit #'series-parallel 2))
(setq circuit (floating circuit))
(when (= (length circuit) len) (return)))
circuit))
I've also added a function floating to remove resistors with only one end connected to the network, which can arise from delta-wye transformations:
(defun floating (l)
(remove-if #'(lambda (x)
(or
(= (countlinks l (first x)) 1)
(= (countlinks l (second x)) 1)))
l))
Testing the new version of solve on the network *c2*:
CL-USER > (solve *c2*) ((D A 32) (A D ?))
and the resistance between a and d is 32Ω.
Finally, try this network containing two deltas:
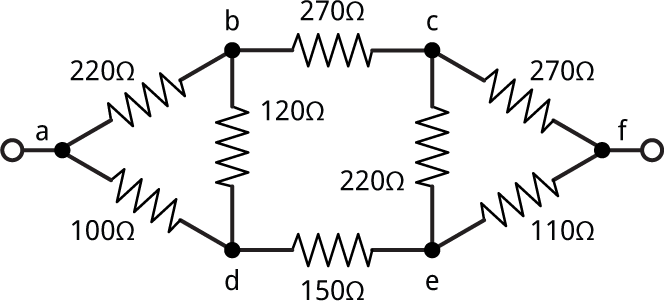
Here's a complete copy of the Lisp program to solve resistor networks: Resistor network program
- ^ Delta-Wye resistor networks on Khan Academy.
blog comments powered by Disqus
