Recursive functions without a base case
19th December 2019
In an earlier post Recursion without a base case I wrote about the fact that it's possible to define a recursive function without an explicit base case. I've recently been exploring some other recursive functions of this sort.
What is a base case?
First of all, to explain what this is all about. The usual definition of a recursive algorithm is that it can be specified by two properties:
- A simple base case: a terminating scenario that does not use recursion to produce an answer.
- A set of rules that reduce all other cases toward the base case [1].
A typical example is the recursive algorithm for factorial:
- factorial(0) is 1, the base case.
- factorial(n) is n * factorial(n-1), reducing all other cases towards the base case.
In Lisp, this is expressed as:
(defun rec1 (n) (cond ((= n 0) 1) (t (* n (rec1 (1- n))))))
A recursive function using multiply
In my earlier post I introduced the following function:
rec(n) = 1 + (n * rec(n-1)).
This is a recursively-defined function with no explicit base case, which actually works fine:
- rec(0) is 1.
- rec(1) is 2.
- rec(2) is 5.
- rec(3) is 16.
and so on. It increases in size rapidly, a bit like factorial.
This is sequence A000522 in the On-Line Encyclopedia of Integer Sequences.
A recursive function using logical AND
In searching for other functions of this type I thought that the logical AND operation could be fruitful, and came up with this:
r(n) = n + (n AND r(n-1))
This can be implemented in Lisp by defining a version of logand that only evaluates its second argument if the first argument is non-zero:
(defmacro ?logand (a b) `(if (zerop ,a) 0 (logand ,a ,b)))
Now r can be defined:
(defun r (n) (+ n (?logand n (r (1- n)))))
Here are the first few values:
> (r 0) 0 > (r 1) 1 > (r 2) 2 > (r 3) 5 > (r 4) 8
It's quite easy to see that r(n) must lie between n and 2n, but its behaviour is quite erratic:
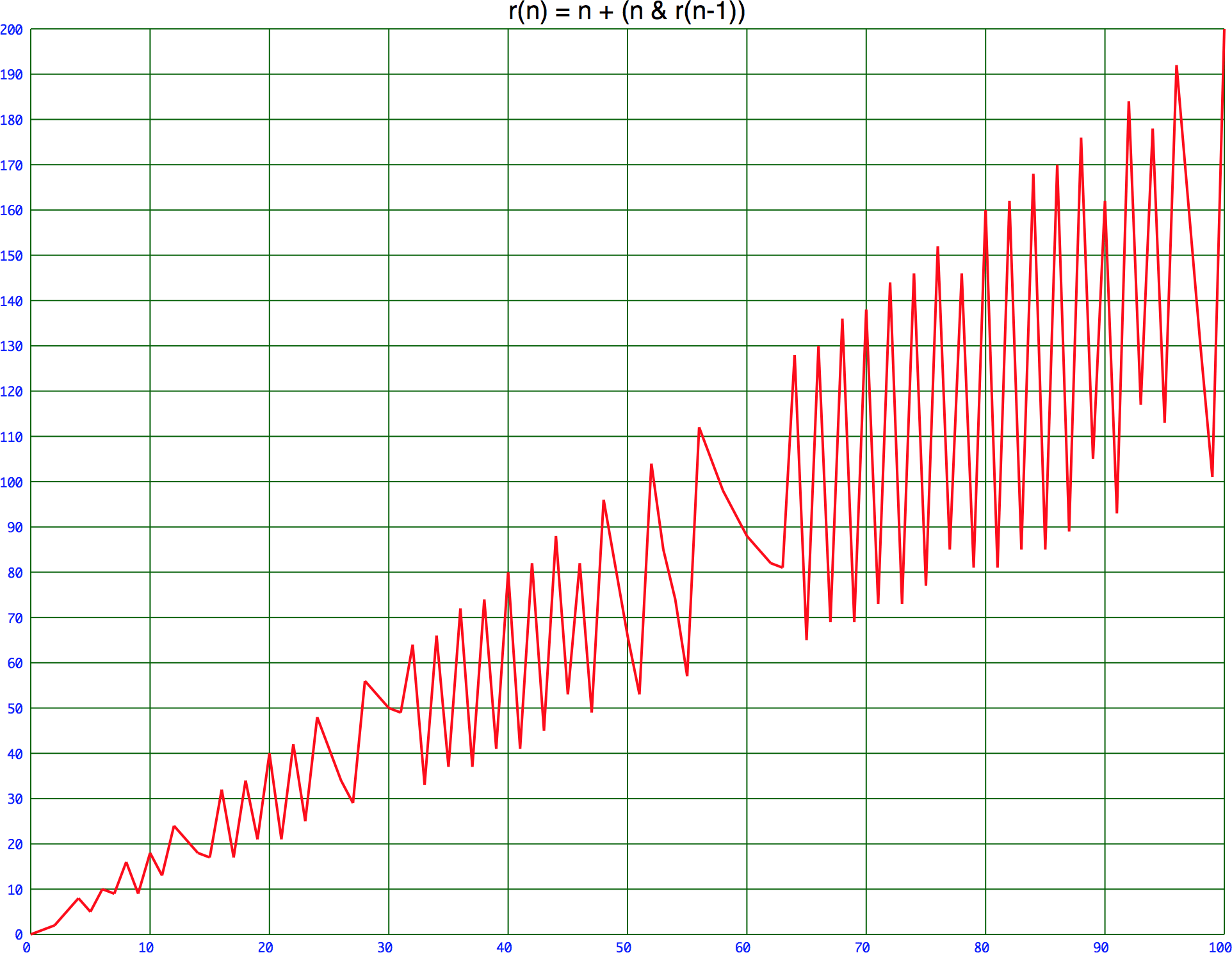
This is sequence A182243 in the On-Line Encyclopedia of Integer Sequences.
A recursive function using exponentiation
Here's another such recursive function:
q(n) = q(n - 1)n + 1
This can be implemented in Lisp by defining a version of expt that only evaluates its first argument if the second argument is non-zero, since anything to the power zero is 1:
(defmacro ?expt (x y) `(if (zerop ,y) 1 (expt ,x ,y)))
Now q can be defined:
(defun q (n) (+ (?expt (q (- n 1)) n) 1))
It grows quite rapidly; here are the first six values:
> (q 0) 2 > (q 1) 3 > (q 2) 10 > (q 3) 1001 > (q 4) 1004006004002 > (q 5) 1020191144865623440455270145683555422808365843606721760320033
This is sequence A330581 in the On-Line Encyclopedia of Integer Sequences.
Update
28th December 2019: N. J. A. Sloane has pointed out that 00 is undefined, so the recursive function using exponentiation does need the explicit base case q(0) = 2.
blog comments powered by Disqus